Crearea intervalelor exponențiale în graficele QlikView™

1 octombrie 2013
Un comentariu
În ciuda multelor funcționalități oferite de QlikView™  zilele astea, am simțit că gândirea unei scale exponențiale pentru crearea de intrervale cu funcția CLASS ar fi o completare drăguță.
 
Mi-a luat câțiva ani să caut o soluție pentru problema asta, iar ieri m-am hotărât ce e de făcut.   😉
 
Așa că asta este: în loc crearea de intervale cu mărginiri egal distanțate, putem crea acum limitele care pot fi definite ca una sau mai multe puteri de 10 (sau orice altceva, desigur).
 
Pentru a fi mai specific, folosind această abordare, se pot defini mărginiri ca 1/10/100/1000/10000/ etc. sau chiar ca 1/1 k/1 mil /etc.
Am folosit pentru toate acestea, pe lângă funcția CLASS, unele egalități și echivalențe de calcul exponențiale și logaritmice de bază.
 
Ca de obicei, atunci când se încearcă dezvoltarea unei anumite funcționalități sau model, în QlikView™ sau în alt software, îmi place să încep cu un prototip care are un set destul de simplu de date în spate.
 
Uneori încarc acest set de date folosint un LOAD*INLINE scurt, în timp ce în alte situații, când este necesar un set de date cu mai multe cazuri, în special unul de care îmi dau seama că va trebui sa-l extind, prefer să folosesc câteva fișiere/foi de Excel ca surse de date.
 
În acest caz, sunt suficiente o singură coloană de date și un singur tabel cu mai multe rânduri, așa ca am folosit abordare INLINE:

LOAD * INLINE [
Dimension
1
2
30
40
50
600
700
800
900
];

După cum puteți observa, acest set de date are 2 valori sub 10, alte trei valori sub 100 și alte 4 valori sub 1000.
 
Am început cu abordarea obișnuită: o dimensiune CLASS (Dimension, BoundaryDistance) calculată și cu o funcție destul de simplă în interiorul expresiei: count(Dimension) aplicat unul grafic de tip bară.
 
Iar acesta mi-a oferit un răspuns ușor de anticipat:
Dar acesta este un mod de vizualizare destul de urât și relativ stupid, corect?!
 
Așa că, deodată ce doream o mărginire egal distanțată exprimată în puteri de 10, am modificat prima formulă în: CLASS (log10(Dimension),1) pentru a vedea ce se întâmplă:
Iar rezultatul, cel puțin din punct de vedere al reprezentării grafice, este deja acolo unde visam să ajung.
 
Cu toate acestea, nu am fost prea mulțumit de etichetele și de textele dimensiunii calculate. Dorința mea era să am text pe dimensiunile apropiate de  0<=Dimension10<= Dimension
 
Pentru aceasta am simțit că trebuie să mă arunc în funcționalitatea DUAL.
 
Dar, încercând să traduc 10<=Dimension mai departe, am realizat că acesta 
 
3.0
 
 
 
este locul, unde 1 și 2 trebuie să fie calculate înainte, pentru fiecare interval, iar apoi să-l calculăm  pe 10  ridicat la fiecare dintre acești exponenți.
 
=> Am modificat dimensiunea calculată în următoarea:
 
=dual(
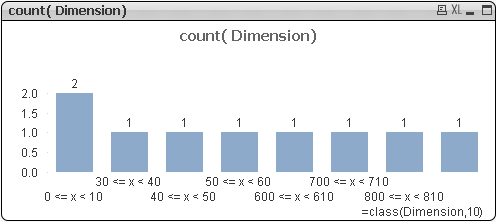
     pow(10,floor(log10(Dimension),1))
          & ‘<=x<‘
          & pow(10,ceil(log10(Dimension),1))
     ,class(log10(Dimension),1, ‘Dimension’)
)
 
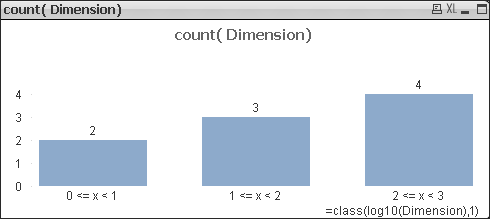
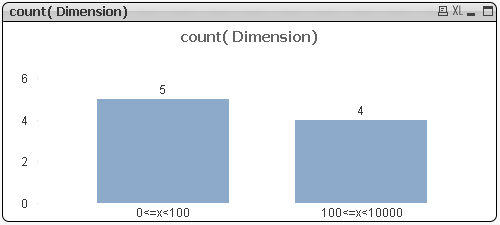
(Am folosit funcțiile FLOOR și CEIL în interiorul QlikView™ pentru a identifica întregii cel mai mici și mai mari imediat următori ai logaritmului.)
 
Această abordare folosind DUAL ne oferă control separat asupra reprezentării numerice și a reprezentării textuale a dimensiunii calculate, și avem următorul rezultat: 

Toate sunt frumoase cu o mică excepție: primul interval pare destul de ciudat! (1<=x<1)

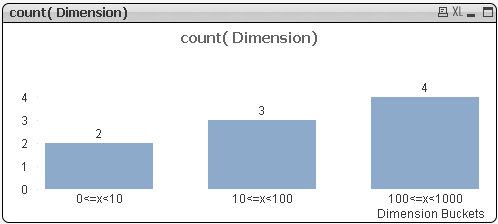
În acest moment, am simțit că ar trebui să înțeleg ce numere sunt de fapt în spatele fiecărei valori din dimensiunea calculată, cât să pot înțelege mai bine ce se întâmplă și am început să mă gândesc la posibilitatea de a muta numerele  tot în zona textului funcției DUAL, posibil folosind funcția NUM() în vârful părții numerice. Dar mi-am amintit că o setare pentru o dimensiune continuă, poate face mai rapid lucruri similare pentru o dimensiune calculată CLASS.

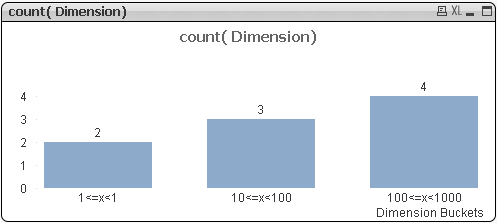
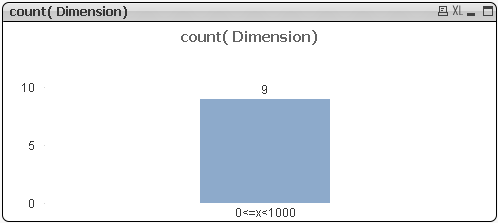
Așa că, numai după ce am verificat opțiunea Continuous odin interiorul Tab-ului  Axes aflat în meniul Properties al graficului și am obținut asta.

Acum, uitându-ne la ultimele 2 imagini, este clar de unde apare problema primului interval: încercăm să folosim log(o) în interiorul pașilor de calcul a primei valori din cadrul primei dimensiuni.
Dar  log(o) este minus infinit și atunci calculul o ia razna!
 
Pentru a rezolva această ultimă problemă, am încercat să folosim mărginirea superioară pentru a identifica cazul și pentru a pune lucrurile în ordine. Următoarea dimensiune calculată pe care am obținut-o este:
 
=dual(
      if( pow(10,ceil(log10(Dimension),1))=1
            , 0&'<=x<‘&10
            ,pow(10,floor(log10(Dimension),1))
                  &'<=x<‘
                  & pow(10,ceil(log10(Dimension),1))
             )
      ,class(log10(Dimension),1)
)
 
și noile grafice (cu Dimensiunea Continuă Primară din nou, nebifată) arată așa:
Aceasta pare o soluție destul de decentă pentru măriginirile intervalului pentru fiecare putere de zece.
 
Totodata, putem merge mai departe și adăuga și opțiunea de a transforma din unități în mii și în milioane, de exemplu.
Pentru aceasta am introdus o variabilă, numită  Variable1, unde pot păstra puterea luizece pe care dorim să o folosim pentru lărgimea ”găleții”.
 
Noua formulă s-a modificat în aceste circumstanțe în:
 
=dual(
     if( pow(10,ceil(log10(Dimension),Variable1))=1
          , 0&'<=x<‘&10
          ,pow(10,floor(log10(Dimension),Variable1))
               &'<=x<‘
               & pow(10,ceil(log10(Dimension),Variable1))
          )
     ,class(log10(Dimension),Variable1     ))
 
iar graficul arată așa pentru Variable=1:

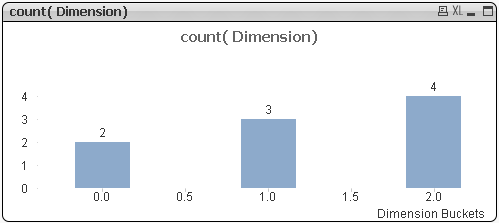
și așa pentru Variable=2:

Realizăm din nou că prima valoare ne joacă niste feste aici.
 
Dar, cu  niște ciupituri adiționale, formula finală făcută în acest prototip este:
 
 =dual(
     if( pow(10,ceil(log10(Dimension),Variable1))=1
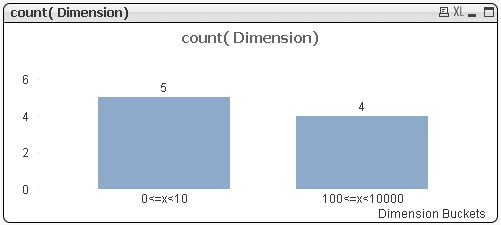
           , 0&'<=x<‘& pow(10,Variable1) ,pow(10,floor(log10(Dimension),Variable1))                    &'<=x<‘                   &pow(10,ceil(log10(Dimension),Variable1))
           )     ,class(log10(Dimension),Variable1
))
 
iar rezultatele, pentru Variable1=1,2 and 3 sunt:
Reflecții finale:
 
  • opțiunea de a calcula dimensiunea în QlikView™ s-a dovedit a fi o opțiune destul de sălbatică și puternica, nu există dubii despre asta!
  • folosirea de prototipuri de date mici de la care să se plece este mereu o idee înțeleaptă!
  • încercați să va ”machiați” formulele și scriptul cât de mult este posibil! (adică structurați-vă codul).
  • CEIL și FLOOR sunt atât de valoroase!
  • salutări funcției LOG10(). Mi-a cam lipsit o variație LOG2() a acesteia într-o serie de limitări deștepte ale mărginirilor Gauge-ului… (dacă e cineva înteresat de acest lucru, anunțați-mă printr-un comentariu 😉 )
Etichete: , , , , , ,